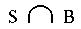Sample Exam I
I. PROBLEM SOLVING.

1. If you have a stair configuration of blocks 12 cubes high at the back and each exposed surface, including the bottom surface, needs to be painted how many square surfaces need painting? (8 points)

2. How many squares are there with corners at points on the following array? (8 points)

3. Add the whole numbers from 1 to 500. (8 points)

II. CONCEPTS.

1. If S is the set of Sophmores at Hard High, and B is the set of students who take Biology, describe the following sets in words? (2 points each)

a) . . .

b) . . .

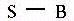c) . . .

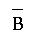d) . . .

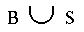2. Given the following sets:

W = {0, 1, 2, 3, 4, 5, 6 }

A = { 0, 2, 4, 6 }

B ={ 1, 2, 3 }

Compute each of the below. ( 2 points each)

a) . . .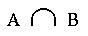

b) . . .

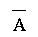c) . . .

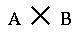d) . . .

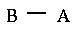e) . . .

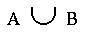3. List all of the subsets of { m, n, o, p }. (6 points)

4. Shade the Venn Diagram to represent . . .

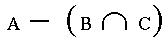(6 points)

5. Identify the shaded portion of this Venn Diagram using set notation. (6 points) . . .

6. Give an example of a set not containing the number 7 that is closed under the operation addition. (4 points)

7. Show by a counter example that - is not a commutative operation. (4 points)

8) Show all possible 1-1 correspondences between { 1, 2, 3 } and { a, b, c } as arrow diagrams. (4 points)

9. Show all possible 1-1 correspondences between { 1, 2, 3 } and { a, b, c } as sets of ordered pairs. (4 points)

10. For each case below, write the number of the whole number property which justifies the statement. (2 points each)

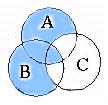
a) 1 x 2 = 2 x 1 1)Closure +
b) 5 + 0 = 5 2)Closure x
c) 7 x (3+5) = (3+5 ) x 7 3)Commutativity +
d) 5 + 3 = 3 + 5 4)Commutativity x
e) 1 x 6 = 6 5)Associativity +
f) 3 x ( 7 + 5 ) = ( 3 x 7) + ( 3 X 5 ) 6)Associativity x
g) 1 + ( 2 + 3 ) = ( 1 + 2 ) + 3 7)Identity +
8)Identity x
9)Distributive Property

11. How many different 1-1 correspondences are there between two six element sets? (4 points)

12. Tell if the following sets are closed under addition. If not, give a counterexample.

(3 points each)

a) { 0, 3, 6, 9, 12, .... }

b) { x | x < 10 }

13. Complete the addition facts table below for base six. (10 points)

14. What are the two numbers before and after 70 in base twelve. (4 points)

____, ____, 70, ____, ____

15. What are the two numbers before and after 37 in base nine. (4 points)

____, ____, 37, ____, ____

16. How many feet are in a mile? _______ (2 points)

17. How many quarts are in a peck? ________(2 points)

III. COMPUTATION.

SHOW YOUR WORK WHENEVER POSSIBLE.

1. Change MCMLXXIX to Hindu-Arabic numerals. (4 points)

2. Change 56374 to each of the following systems. (6 points each)

a) Myan

b) Babylonian

c) Egyptian

3. Write in Hindu Arabic numerals each of the following numbers: (6 points each)

a) Babylonian . . .

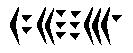b) Myan . . .

c) Myan . . .

4. Calculate the following by the algorithm of your choice in Base seven. (Do not convert to base 10) (6 points)

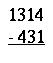5. Divide in base six. (6 points)

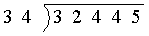34 x 1 = 34

34 x 2 = 112

34 x 3 = 150

34 x 4 = 224

34 x 5 = 302

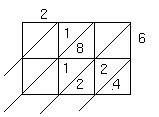
6. Find the missing values in the base ten lattice multiplication problem shown below. Then find the product. (6 points)

7. Change 5492 to base nine notation. (4 points)

8. Change 2322(four) to base ten notation. (4 points)

9. Calculate in base ten by the complement method, (4 points)

3 2 5

- 1 5 6

10. Multiply 3 4 by 4 2 in base eight. (4 points)

11. Multiply 3 4 by 4 2 in base eleven. (4 points)